Overview

The T41 V12 radio has a bandpass filter board with 9 different filter channels. Each channel has 5 inductors that need to be wound around a toroidal core to achieve the desired inductance. I carefully measured the inductance of each component and tweaked them by hand to get the nicest looking passband I could.

Table

The table below shows the number of windings N on each core for each inductor, the inductance I measured (see methods below), and the desired inductance from the Elsie model.

Band	Inductors	Core	N	L measured	L goal
6m	L601,L605	Air	5	not measured	39 nH
6m	L602,L604	T37-10	16	730 nH	720 nH
6m	L603	Air	7	not measured	24 nH
12&10m	L501,L505	T37-0	12	110 nH	120 nH
12&10m	L502,L504	T37-10	17	750 nH	820 nH
12&10m	L503	T37-0	10	85 nH	82 nH
17&15m	L401,L405	T37-0	14	148 nH	150 nH
17&15m	L402,L404	T37-10	21	1140 nH	1200 nH
17&15m	L403	T37-0	10	85 nH	82 nH
20m	L301,L305	T37-0	17	198 nH	220 nH
20m	L302,L304	T37-6	25	1845 nH	2200 nH
20m	L303	T37-0	12	110 nH	120 nH
30m	L291,L295	T37-0	19	236 nH	245 nH
30m	L292,L294	T37-10	38	3639 nH	3600 nH
30m	L293	T37-0	13	127 nH	132 nH
40m	L201,L205	T37-0	32	558 nH	560 nH
40m	L202,L204	T37-1	22	3888 nH	3900 nH
40m	L203	T37-0	23	329 nH	330 nH
60m	L191,L195	T37-10	17	750 nH	840 nH
60m	L192,L194	T37-1	26	4985 nH	5200 nH
60m	L193	T37-2	9	394 nH	400 nH
80m	L101,L105	T37-10	20	1035 nH	1000 nH
80m	L102,L104	T37-1	27	5550 nH	5600 uH
80m	L103	T37-0	32	558 nH	560 nH
160m	L91,L95	T37-6	26	1974 nH	2000 nH
160m	L92,L94	FT37-61	15	10619 nH	11000 nH
160m	L93	T37-10	20	1035 nH	1000 nH

Plots

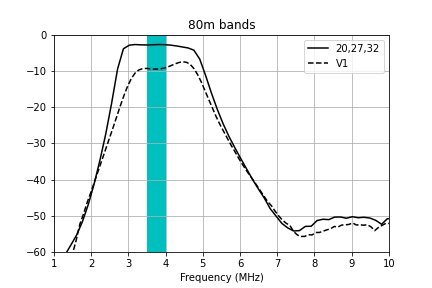
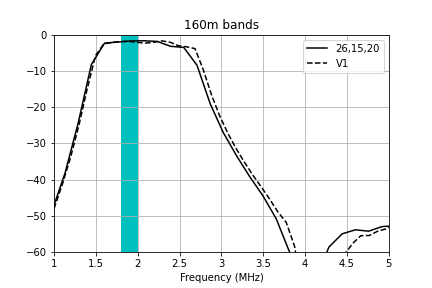
The measured passband for each of the filter channels is plotted below.

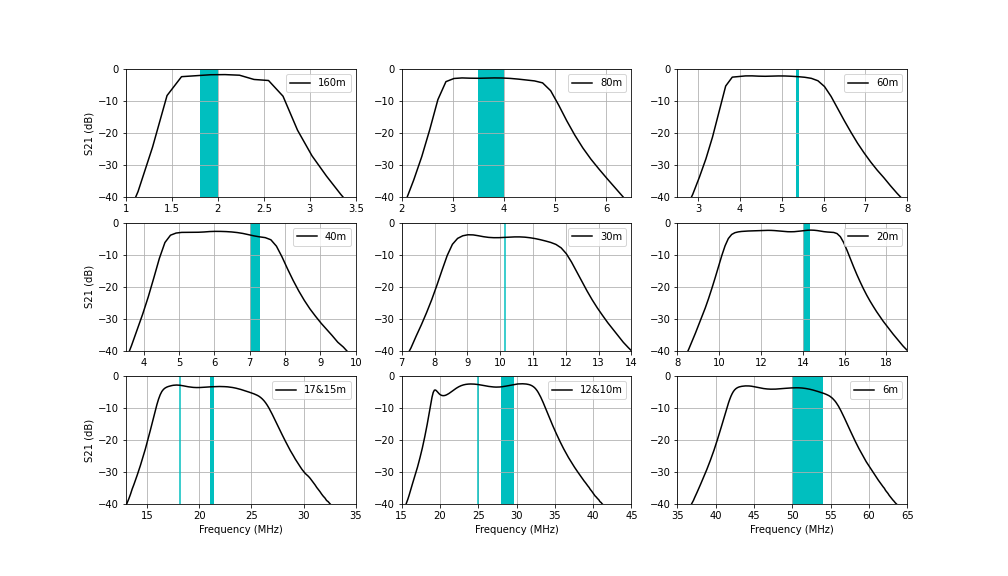
Here are zoomed-in plots that compare the measured transmission to the Elsie simulation and my prior attempt at winding the filters (V1) for each of the bands. The windings specified in the table above give very good performance that matches the Elsie simulations fairly well.

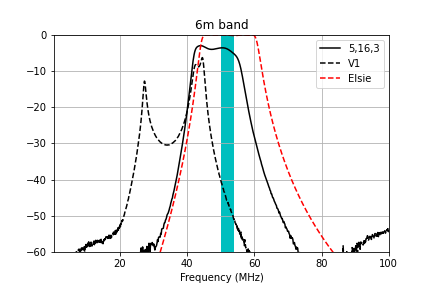
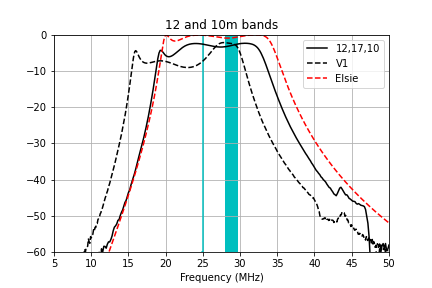
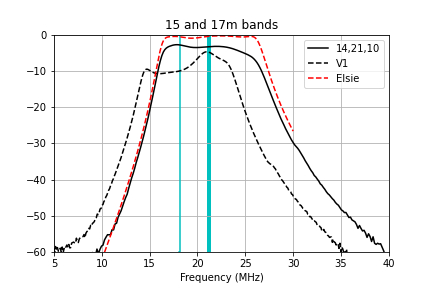
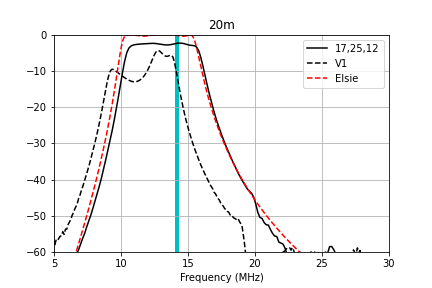
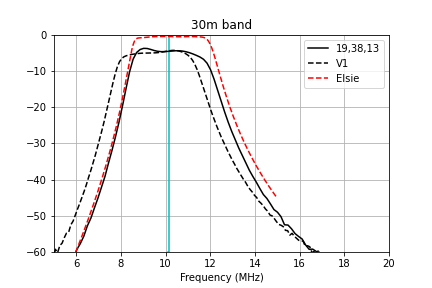
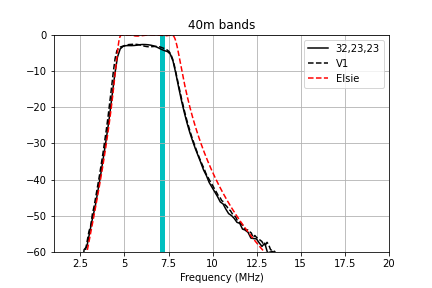
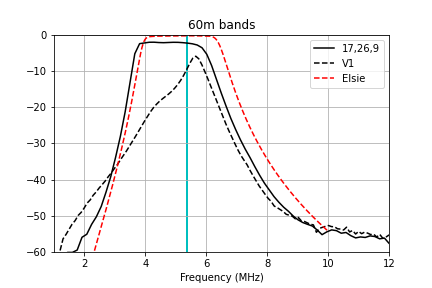
Methods

I measured the inductance of each toroid using one of two methods.

Direct measurement with a VNA

Use a ZIF socket soldered to a PCB to hold the inductor. Using SMA connectors, place the inductor in a series circuit as shown below.

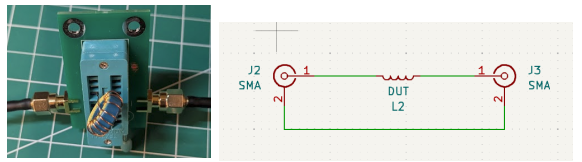
I use the NanoVNA-Saver software and a NanoVNA to measure the inductance of the fixture and device under test (DUT). Note that the VNA must be calibrated. NanoVNA will calculate the equivalent series inductance for you.

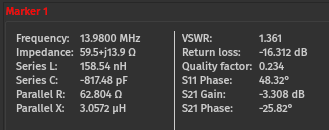
You can also export the measured response as a Touchstone s2p file. I then use Python and the scikit-rf library to calculate the equivalent series inductance from the magnitude of the imaginary part of S[1,1]:

import skrf as rf
def calculate_L_nH(S):
    return (S.s11.z_im.flatten())/(2*rf.pi*S.f)*1e9
S = rf.Network('file.s2p')
L_nH = calculate_L_nH(S)

It looks something like this:

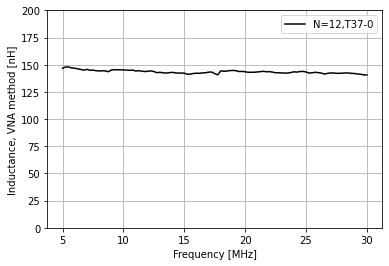
It’s critical to note that this measurement includes the inductance of the test fixture! The fixture inductance needs to be subtracted to obtain the DUT inductance. I measure the test fixture inductance by placing a short conductor between the terminals of the ZIF socket; I measured it to be 30 nH.

It’s also important to note that the ZIF socket has an equivalent series capacitance of roughly 4 pF (again measured using a NanoVNA). The resonance frequency between the ZIF socket capacitance and the inductor under test approaches HF frequencies for high inductance values, which gives false readings using this method. Based on testing, I’ve concluded that measuring inductor values above 2 uH is unreliable using the VNA method and this particular test fixture. For such inductors I use the resonance method.

Resonance method

In this method, place a capacitor in parallel with the inductor under test and measure the frequency of the minimum in the transmitted signal S21.

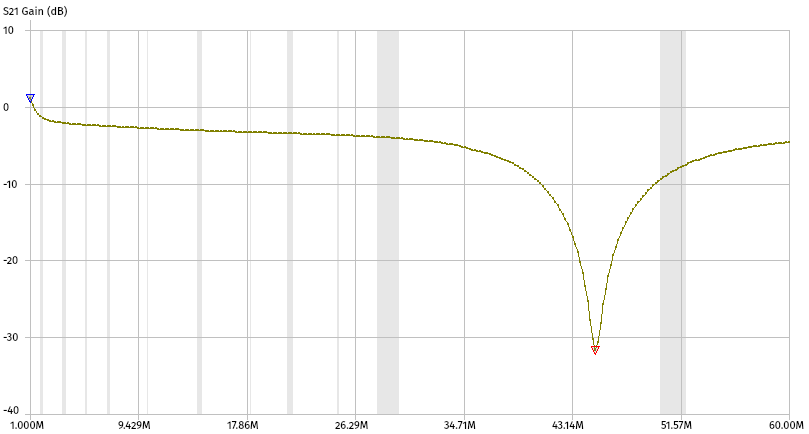
This frequency is the resonance frequency of the tank circuit formed by the inductor under test and the reference capacitor. The exact capacitance of the reference capacitor can be found by measuring the equivalent series capacitance of the capacitor when placed in the ZIF socket using the NanoVNA software. It should be higher than the listed value of the capacitor due to the ZIF socket’s parasitic capacitance.

Once you have the resonance frequency, calculate the inductance using this formula:

\[L_{\rm DUT} = \frac{1}{C_{\rm ref}(2 \pi f_{\rm res} )^2}\]

Note that you do not need to subtract the inductance of the test fixture when using this method – its inductance doesn’t become part of the resonating circuit.